인공지능시스템 03 문제풀이 (2)

 

 

경험적 탐색

 

 

1. 경험적 탐색

: 목표상태를 보다 신속하게 탐색하기 위해

경험적인 정보를 활용하는 탐색 방법

 

- 경험적 탐색은 목표상태를 보다 효과적으로 탐색하기 위해 경험적 지식을 평가함수에 반영

* 평가함수: 어떤 상태가 주어졌을 떄 그 상태를 거쳐 가는 것이 목표상태로 가는 데 얼마나 바랍직한가를 나타내는 함수

-> 해를 향해 가는 데 필요한 비용, 해로 향하는 경로 상에 존재할 가능성 등

 

 

2. 평가함수

 

1) 평가함수의 구성 요소

: 출발노드 S에서 출발해 노드 n까지 도착했을 때,

노드 n의 평가함수의 정의에 포함될 수 있는 비용

- g(n): 출발 노드 S로부터 현재상태를 나타내는 노드 n까지 도달하는 데 소비한 경로비용

- h(n): 노드 n으로부터 목표노드 G까지 도달하는 데 필요한 경로비용

-> ĥ(n): 경험적 지식을 이용해 h(n)을 예측한 비용

 

=> 탐색 알고리즘에 따라서 이 요소 중 어떤 것을 어떻게 사용할 것인지가 다름

 

 

언덕오르기 탐색

 

 

1. 언덕오르기 탐색 알고리즘

 

1) 탐색순서

- 임의의 상태에서 시작하여 가장 목표에 근접한 후계상태로 이동하는 탐색 알고리즘

- 현재상태를 확장하여 생성된 후계노드들 중에서 다음 확장할 노드를 선택함

(깊이우선 탐색과 유사한 순서로 탐색)

- 후계노드의 평가함수를 계산하여 비용이 가장 적은 노드를 다음 확장할 노드로 선택

(* 노드의 비용: 그 노드로부터 목표노드에 도달하는 비용을 예측한 값)

 

2) 평가함수

- 후계노드로부터 목표노드에 도달하는 비용을 예측한 값

- 후계노드까지 도달하는 데 사용된 비용은 고려하지 않음

 

 

2. 8-퍼즐 문제

 

- 초기상태에서 목표상태까지 가는 상태의 비용: 목표상태의 퍼즐과 비교했을 때 지정된 위치에 존재하지 않는 조각의 수

-> ex. 제 자리에 있지 않은 조각의 수가 4개일 때 초기상태의 비용은 4로 정의

 

 

3. 최적화 문제: 등산 문제

어떤 사람이 초행길의 산을 등산하는 도중 짙은 안개를 만났다. 지도도 없고, 사람이 다닌 길도 없으며, 오직 나침반에만 의지하여 산에 올라간다. 정상에 도달하려면 어떻게 해야 하는가?

- 상태: 등산가의 좌표 및 고도

- 연산자: 동, 서, 남, 북 방향으로 정해진 거리만큼 이동

- 목표상태: 모든 후계상태의 고도가 현재상태보다 낮은 상태(어느곳으로 이동하더라도 더 높은 곳으로 갈 수 없다면 현재 위치가 정상이라고 판단)

 

-> 등산 문제의 탐색으로 이동하는 경로는 현 위치에서 이동할 수 있는 가장 높은 곳으로 이동하는데, 경사가 가장 가파른 방향으로 움직여 가장 큰 평가함수 값을 갖는 상태로 향해 가는 것이므로 최급상승법(steepest ascent)이라고 한다.

* 만일 평가함수 값이 가장 작은 상태를 찾는 경우는 최급하강법(steepest descent)이라고 한다.

 

* 최급상승법(또는 최급하강법)은 최적 해를 구하는데 실패하는 경우
① 지역최대치 문제: 실제 정상보다 낮은 다른 봉우리에 도달하였을 때 이를 정상으로 잘못 판단

(** 시스템의 최대치에 해당되는 계수를 찾는 문제에서 실제 최대치가 아니라 주변의 극대치에 해당되는 계수를 찾게 되는 문제)
② 고원 문제: 현 상태를 개선할 방법이 없어 탐색을 진행하지 못하는 문제
③ 능선 문제 : 연산자 집합이 모든 변화 방향을 충분히 수용하지 못할 경우 현재 상황을 개선하지 못해 탐색에 실패

(등산가 문제에서 동, 서, 남, 북 방향의 움직임만 고려하고 북동, 동남, 남서, 서북 방향의 이동은 고려하지 않을 경우 탐색에 실패함)

 

 

모의 담금질(simulated annealing)

* annealing(풀림): 금속이나 유리를 일정한 온도로 가열한 다음 천천히 식혀 내부 조직을 고르게 하고 응력을 제거하는 열처리 조작

 

 

1. 모의 담금질(simulated annealing)

: 평가함수의 값이 전역최소치(또는 전역최대치)에 해당되는 해를 구하기 위한 확률적 접근방법

 

- 현재 상태를 개선하지 않는 후계상태로도

- 시간에 따라 감소하는 확률에 따라 평가함수의 값이 증가하는 후계상태로도 이동할 수 있게 함으로써

- 지역최대치(최소치)에서 빠져나올 수 있게 하는 확률적 접근방법

 

 

2. 모의 담금질 알고리즘

 

// temperature(t): 시간 t에 따른 온도를 나타내며, 
//                  t에 따라 서서히 감소하도록 함 
// 					h(s) : 상태s에 대한 평가함수
현재상태 = 문제의 초기상태;
for t=1 to ∞ do
	T = temperature(t);
	if T == 0 then
		return 현재상태;
	end-if;

	차기상태 = 현재상태의 후계노드 중에서 임의로 선택;
	ΔE = h(차기상태) - h(현재상태);
	if ΔE > 0 then
	현재상태 = 차기상태;
	else
	확률 eΔE/T에 따라 차기상태를 현재상태로 선택; 
    end-if;
end-for;

 

 

A* 알고리즘

 

 

1. A* 알고리즘

: 다음 확장할 노드를 결정할 때 그 노드까지 도달하는 경로비용과 그 노드로부터 목표노드에 도달하기 위한 경로비용 예측치의 합이 최소인 노드를 선택하여 탐색하는 방법

- A* 알고리즘에서는 평가함수가 최소인 노드를 선택하여 확장한다.

- 예측비용이 항상 실제 비용 이하로 예측되도록 정의한다면 탐색된 경로는 최소비용 경로이다.

 

 

2. A* 알고리즘의 평가함수

: 출발노드로부터 그 노드에 도달하기 위한 비용과 그 노드로부터 목표노드에 도달하는데 필요한 예측비용의 합

 

1) 평가함수의 구성 요소

: 노드 n까지 도달한 상태에서 출발노드 S에서 노드 n을 거쳐

목표노드 G까지 도달하는 전체 경로의 비용 계산

- g(n): 출발 노드 S로부터 현재상태를 나타내는 노드 n까지 도달하는 데 소비한 경로비용

- h(n): 노드 n으로부터 목표노드 G까지 도달하는 데 필요한 경로비용

- ĥ(n): 노드 n으로부터 목표노드 G까지 도달하는 데 드는 비용의 예측치

-> 평가함수 f̂(n): 실제 비용 f̂(n)의 예측치

f̂(n) = g(n)+ ĥ(n)

 

=> 균일비용탐색에서는 g(n)을 사용하고

=> 언덕오르기탐색에서는 ĥ(n)을 사용하며

=> A* 알고리즘에서는 둘을 결합해 이 비용 전체를 사용한다

 

 

3. A* 알고리즘

 

1) 출발노드 S를 OPEN에 삽입(평가함수 f̂(S)를 계산하여 첨부)
2) OPEN에 남은 노드가 있으면 아래를 반복

  ① OPEN에서 f̂ 이 최소인 노드 n을 꺼내 CLOSED에 넣는다.
  ② 노드 n이 목표노드라면 탐색성공
  ③ 노드 n을 확장하여 후계노드 n1, n2, ⋯, nm을 생성

  ④ 후계노드의 평가함수 f̂(n1), f̂(n2), ⋯, f̂ (nm)을 계산

  ⑤ 후계노드 n 𝑖 , 𝑖 = 1, 2, ⋯, 𝑚을 OPEN에 삽입

      (중복 생성된 노드 제거)
3) 탐색 실패

 

<중복 생성된 노드 nnew의 처리>

- 동일한 상태(노드nold)가 OPEN에 존재하는 경우 -> 아직 어느 노드도 확장되지 않은 상태이므로 평가함수 f̂이 큰 노드를 제거하면 됨

- 동일한 상태(nold)가 CLOSED에 존재하는 경우   ① f̂ nold ≤ f̂ nnew인 경우   -> 아직 어느 노드도 확장되지 않은 상태이므로 평가함수 f̂이 큰 노드를 제거   ② f̂ nold ＞ f̂ nnew인 경우   -> nnew를 제거하면 됨   -> nnew를 제거하되 nold의 부모노드 포인터가 nnew의 부모노드를 가리키도록 수정   -> nold 및 nold의 후계노드들의 평가함수 값을 갱신

 

 

4. A* 알고리즘에서 탐색된 경로가 최소비용경로가 되기 위한 조건

 

: 만일 어떤 노드로부터 목표노드까지 도달하는 값이

경로비용을 예측한 값이 항상 실제 비용 이하라면(즉, 항상 ĥ(n) ≤ h(n)이 성립),

A* 알고리즘은 최소비용 경로를 탐색하는 것을 보장한다.

 

 

5. 8퍼즐 문제의 풀이

: 8-퍼즐 문제에 A* 알고리즘을 적용

 

- g(n): 빈 칸의 이동 횟수

- ĥ(n): 목표상태의 퍼즐과 비교했을 때 지정된 위치에 존재하지 않는 조각의 수

 

 

6. 경로 탐색 문제의 풀이

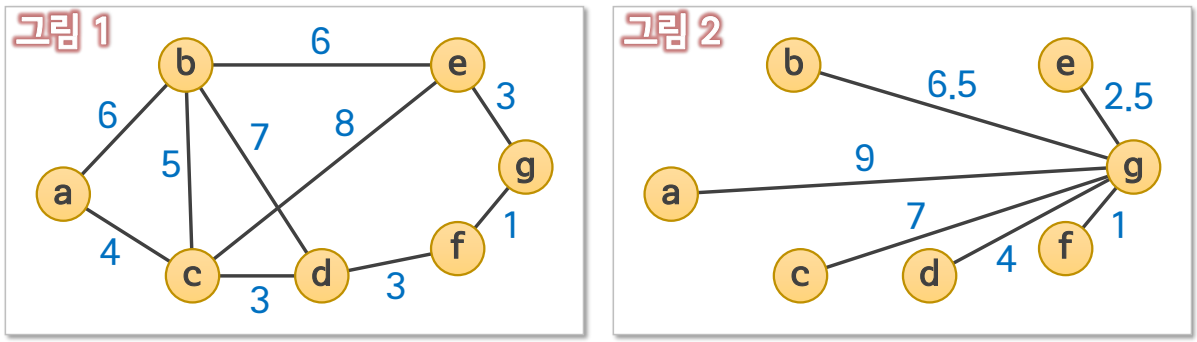
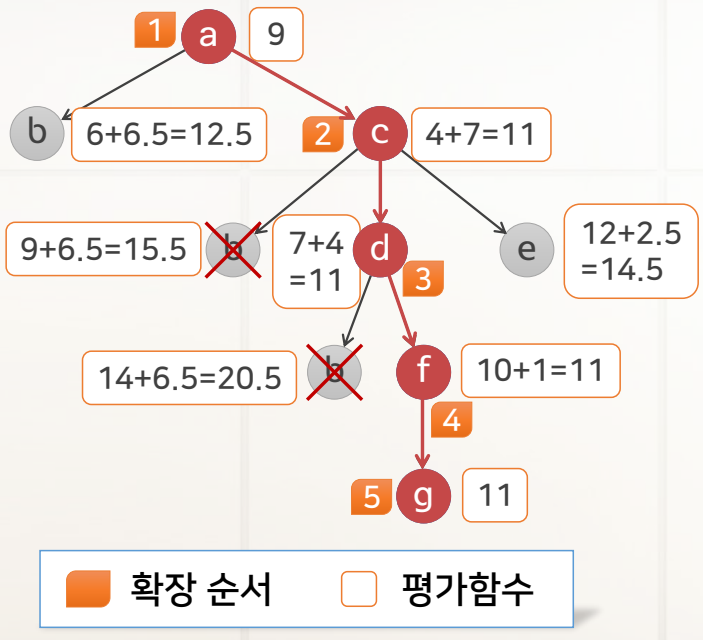
a, b, c, d, e, f, g라는 7개의 도시를 연결하는 도로망이 건설되어 있다. 어떤 여행자가 도시a를 출발하여 도시g까지 가는 경로를 찾고자 한다. 그림1은 각 도시를 연결하는 도로와 그 거리를 표현한 그래프이고, 그림2는 각 도시로부터 목적지인 g까지의 직선거리이다. A* 알고리즘을 이용하여 최단길이 경로를 탐색하라.

 

 

---

 

 

경험적 탐색은 경험적 지식을 활용하여 문제의 해를 보다 효과적으로 탐색하기 위한 기법이다. 경험적 지식을 탐색에 적용하는 방법 및 주요 경험적 탐색 방법, 탐색을 통해 성공적으로 목표를 달성하는데 장애가 되는 요소와 이 문제를 개선하기 위한 탐색 기법을 모색해야 한다.