인공지능시스템 02 문제풀이 (1)

 

 

문제풀이

 

 

1. 문제풀이의 개념

 

:직관적으로 단순하게 해결할 수 없는 문제에 대해

문제를 파악하고 문제의 해에 이르는 방법을 찾아내는 일련의 과정

 

문제풀이에 사용될 수 있는 전략: 경험적 방법

 

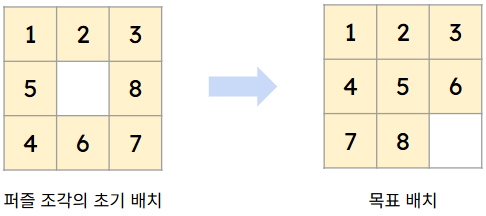
EX 1. 8-퍼즐 문제

 

EX 2. 하노이 탑 문제

 

 

문제의 표현

 

 

1. 문제의 상태를 컴퓨터로 표현

 

상태(state): 퍼즐 조각 배치 형태

↓

* 상태묘사(state description): 풀이하고자 하는 문제의 상태를 컴퓨터로 처리하기 위한 적절한 자료구조로 표현한 것

↓

초기상태: 최초에 주어진 문제의 상태

↓

목표상태: 풀이된 결과에 해당되는 문제의 상태

↓

연산자(operator): 문제의 어느 한 상태로부터 변화할 수 있는 다른 상태로 변환하는 도구로서, 변환 테이블이나 변환 함수로 구현함

 

 

 

2. 상태묘사

: 풀이하고자 하는 문제의 상태를 컴퓨터로 처리하기 위한 적절한 자료구조로 표현한 것

 

문제에 따라 적절한 자료구조를 선택

- 문제의 상태를 표현하는 데 보다 자연스러운 표현 방법

- 하나의 상태묘사에서 다른 상태묘사로 변화시키는 연산이 용이한 표현

-> 기호 열, 벡터, 다차원 배열, 트리, 리스트 등

 

EX 1. 8-퍼즐

↓ 2차원 배열로 표현

struct PuzzleState {
	int blankX, blankY;
    char board[3][3];
};

 

 

3. 연산자

 

1) 연산자의 역할

: 어느 한 상태로부터 변화할 수 있는 다른 상태로 변환함

 

2) 연산자의 정의

- 변환 테이블을 정의하는 방법: 모든 '입력' 상태묘사에 대해 각각의 상태로부터 변화할 수 있는 모든 '출력' 상태묘사를 저장하는 목록을 만듦

- 일반화된 변환 규칙으로 정의하는 방법: 하나의 상태묘사를 다른 상태묘사로 변화시키는 일종의 연산 능력을 지닌 함수로 정의

 

EX 1. 8-퍼즐

퍼즐의 배열을 바꾸는 방법: 빈칸을 옮긴다

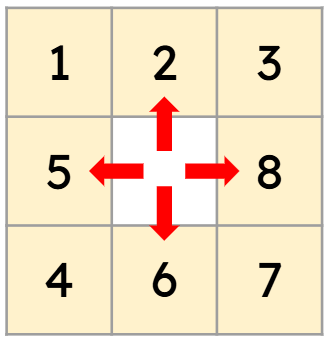
테이블 배치 형태로 로직을 구성할 수 있다(행렬)

int opMvBlnkUp(PuzzleState* s) {
	if (s->blankY > 0) {
		s->board[s->blankX][s->blankY] =
			s->board[s->blankX][s->blankY-1];
        s->board[s->blankX][--s->blankY] = ' ';
        return 1;
	}
	else 
    	return 0;
}

 

 

4. 상태 사이의 관계 표현

: 방향성 그래프를 이용해 부모상태와 후계상태의 관계 표현

 

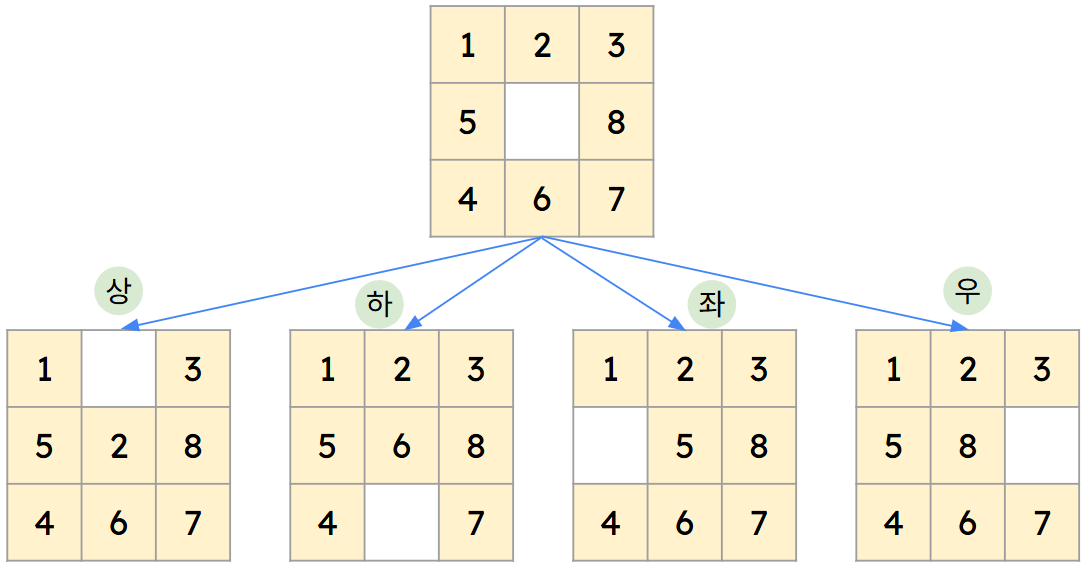
- 부모상태: 원래의 상태

- 자식상태(후계상태): 그로부터 파생된 상태

- 상태공간: 이런식으로 초기상태로부터 얻을 수 있는 모든 상태의 집합

* 상태공간: 정의된 연산자 집합을 이용하여 초기상태로부터 얻을 수 있는 모든 상태의 집합으로, 그래프 형태로 표현할 수 있다.

 

 

5. 상태공간에서의 문제 표현

: 상태묘사 및 초기상태의 정의, 목표상태의 정의, 연산자의 정의를 함으로써 상태공간에서 문제를 표현한다.

 

< 표기해야 할 문제를 표현하는 순서 >

1) 상태묘사 및 초기상태 정의

2) 목표상태 정의

3) 연산자 정의

 

EX 1.

4리터들이 물병과 3리터들이 물병이 한 개씩 있다. 이 병에는 양을 측정할 수 있 는 눈금이 없으며, 항상 물을 공급할 수 있는 펌프가 있다. 4리터들이 물병에 정확히 2리터의 물을 채워라.

 

1) 상태묘사 및 목표상태 정의

: 초기상태(0,0) -> 목표상태(2,0)

 

2) 연산자 정의

연산자	현 상태	차기 상태	의미
1	(x, y), x<4	(4, y)	4리터들이 물병을 채움
2	(x, y), y<3	(x, 3)	3리터들이 물병을 채움
3	(x, y), x>0	(0, y)	4리터들이 물병을 채움
4	(x, y), y>0	(x, 0)	3리터들이 물병을 채움
5	(x, y), x<4 and x+y>=4	(4, x+y-4)	3리터들이 물병의 물을 4리터들이 물병이 가득 찰 때까지 옮김
6	(x, y), x<3 and x+y>=3	(x+y-3, 3)	4리터들이 물병의 물을 3리터들이 물병이 가득 찰 때까지 옮김
7	(x, y), x+y<4 and y>0	(x+y, 0)	3리터들이 물병에 남은 물을 4리터들이 물병에 모두 옮김
8	(x, y), x+y<3 and x>0	(0, x+y)	4리터들이 물병에 남은 물을  3리터들이 물병에 모두 옮김

 

-> 상태공간을 도형으로 표시할 수 있다

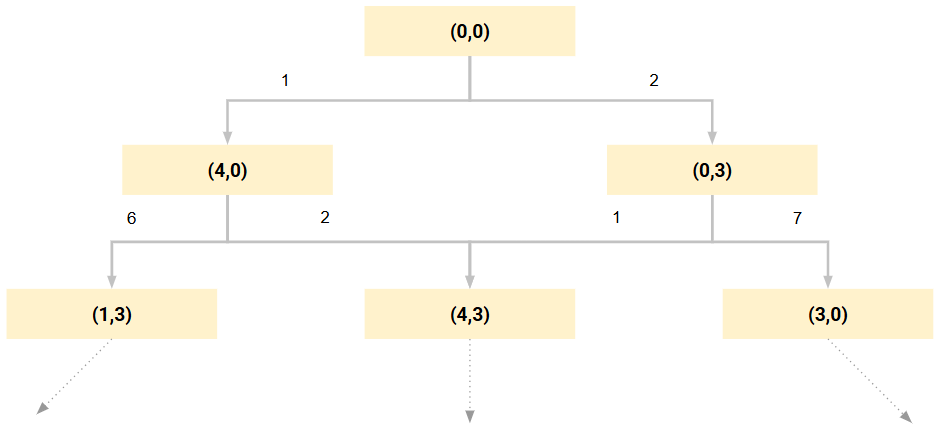
-> 상태공간이라는 것은 그래프 형태가 될 수 있다

 

 

상태공간 탐색에 의한 문제풀이

 

 

1. 상태공간에서의 문제풀이

 

- 초기상태에서 시작해 목표상태에 도달할 수 있는 일련의 연산자를 찾는 것

-> 그래프에서의 경로의 탐색

 

- 시행착오를 거치면서 초기상태로부터 목표상태에 도달하는 경로 탐색

 

- 탐색에 유용한 지식을 사용함으로써 방대한 상태공간에서 탐색 범위를 좁히려고 하는 것

 

 

2. 탐색 과정

 

- 정해진 기준에 따라 노드를 선택

 

- 노드의 확장

-> 그래프 탐색에서 선택된 노드(상태)에 적용할 수 있는 모든 연산자를 가하여 모든 후계노드(후계상태)를 생성

 

- 후계노드에 부모노드를 가리키는 포인터를 첨부

-> 탐색에 성공한 후 풀이 경로를 알 수 있게 함

 

- 목표노드가 있는지 검사함

 

- 원하는 목표를 찾지 못했다면 정해진 기준에 따라 다음 노드를 선택하여 탐색 과정 반복

 

- OPEN: 앞으로 확장할 노드를 저장하는 리스트

- CLOSE: 이미 확장한 노드를 저장하는 리스트

 

- 탐색 알고리즘에 따라 정해진 순서로 OPEN에서 노드를 꺼내고, 확장된 노드를 OPEN의 적절한 위치에 저장함

 

 

탐색 방법의 종류

 

 

1. 맹목적 탐색(blind search)

: 다음 확장할 노드를 선택할 때 목표노드의 위치에 대한 정보를 사용하지 않고 정해진 순서에 따라 탐색하는 방법

 

- 목표노드의 위치와 무관한 순서로 노드 확장

- 소모적인 탐색을 할 가능성이 있음

 

 

2. 경험적 탐색(heuristic search)

 

: 문제영역에서 사용할 수 있는 목표노드의 위치와 관련된 경험적 정보를 사용하는 탐색 방법

 

- 경험적 정보: 항상 옳은 것은 아니지만, 개연성이 있어 많은 경우 잘 맞는 정보

 

 

탐색의 목적 및 경험적 정보 사용에 따른 분류

 

 

정보사용 / 목적	임의 경로 탐색	최적 경로 탐색
맹목적 탐색	깊이우선 탐색 너비우선 탐색	균일비용 탐색
경험적 탐색	언덕오르기 탐색 최적우선 탐색 모의 담금질	A*알고리즘

 

 

1. 깊이우선 탐색

 

- 탐색 진행방향(깊이 방향)으로 계속 전진하여 목표를 탐색하는 방법

-> 가장 최근에 생성된 노드를 가장 먼저 확장함

-> OPEN은 스택 구조

 

- 목표에 도달할 수 없는 경로를 계속 탐색하게 될 수 있음

-> 깊이 제한(depth bound)을 정할 수 있음

 

- 깊이제한에 도달하거나 더 이상 진행 경로가 없을 경우

-> 이전 상태 중 다른 경로를 선택할 수 있는 위치로 복귀하여 탐색을 계속함

 

<깊이우선 탐색 알고리즘>

출발노드를 OPEN에 삽입; 
while not empty(OPEN) do
	n = OPEN의 제일 앞 노드;
	n을 OPEN에서 제거하여 CLOSED에 넣음;
	if depth(n) < 깊이제한 then
		노드n을 확장하여 모든 후계노드를 생성;
		생성된 후계노드들에게 부모노드 n을 가리키는 포인터를 첨부;
		if 후계노드 중 목표노드가 존재 then
			그 후계노드로부터 포인터를 역으로 추적하여 풀이경로 구성;
			return 탐색성공;
		else
			후계노드를 OPEN의 앞에 넣음;
		end-if;
	end-if;
end-while;
return 탐색실패;

 

 

 

2. 너비우선 탐색

 

- 트리의 레벨 순서에 따라 노드를 확장함

-> 생선된 순서에 따라 노드를 확장함

-> OPEN은 큐 구조

 

<너비우선 탐색 알고리즘>

출발노드를 OPEN에 삽입; 
while not empty(OPEN) do
	n = OPEN의 제일 앞 노드;
	n을 OPEN에서 제거하여 CLOSED에 넣음;
	노드n을 확장하여 모든 후계노드를 생성;
	생성된 후계노드들에게 부모노드 n을 가리키는 포인터를 첨부;
	if 후계노드 중 목표노드가 존재 then
		그 후계노드로부터 포인터를 역으로 추적하여 풀이경로 구성;
		return 탐색성공;
	else
		후계노드를 OPEN의 뒤에 넣음;
	end-if;
end-while;
return 탐색실패;

 

 

 

3. 균일비용 탐색

 

: 상태의 이동에 따른 비용이 다를 수 있다

 

- 노드 사이의 경로비용

- 한 상태에서 다른 상태로 이동하기 위해 필요한 '비용'

 

<균일비용 탐색 알고리즘>

출발노드를 OPEN에 삽입, 출발노드의 경로비용은 0;
while not empty(OPEN) do
	n = OPEN의 제일 앞 노드;
	n을 OPEN에서 제거하여 CLOSED에 넣음;
	if n == 목표노드 then
		노드 n으로부터 포인터를 역으로 추적하여 풀이경로 구성;
		return 탐색성공;
	end-if;
	노드 n을 확장하여 후계노드 n1, n2,···,nm을 생성;
	for i=1 to m do
		ni에 부모노드인 n을 가리키는 포인터 첨부;
		ni의 경로비용 g(ni)를 계산;
	if ∃nold (nold∈OPEN and nold == ni) then
		if g(nold) > g(ni) then
			nold를 ni로 대체; // 비용이 더 큰 기존 경로를 제거
		else
			ni를 제거; // 비용이 더 큰 새로운 경로를 제거
		end-if;
	else if ∃nold (nold∈CLOSED and nold == ni) then
		ni를 제거; // g(ni)는 g(nold)보다 작을 수 없음
	else
		ni를 OPEN에 추가;
	end-if;
	end-for;
	OPEN을 경로비용 g의 오름차순으로 정렬;
end-while;
return 탐색실패;

 

EX 1.

a, b, c, d, e, f, g라는 7개의 도시를 연결하는 도로망이 건설되어 있다. 어떤 여행 자가 도시a를 출발하여 도시g까지 가는 경로를 찾고자 한다. 다음 그림은 각 도시를 연결하는 도로와 그 거리를 그래프로 표현한 것이다. 균일비용 탐색을 하여 최단길 이 경로를 탐색하라.

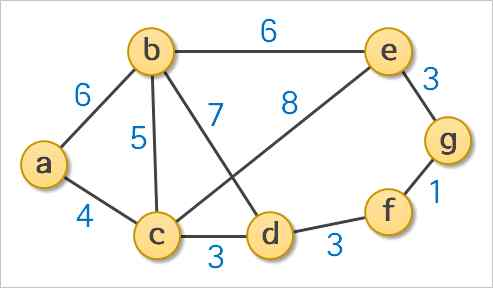
<풀이순서>

a>c(4)>b(9) : a에서 b까지 가는 더 빠른 방법이 있음(6)

a>c(4)>d(7)>f(10)>g(11) : 가장 적은 비용 -> 최소비용경로

a>c(4)>e(12)>g(15) : a에서 g까지 가는 더 빠른 방법이 있음(11)

 

a>b(6)>c(11) : a에서 c까지 가는 더 빠른 방법이 있음(4)

a>b(6)>d(13)  : a에서 d까지 가는 더 빠른 방법이 있음(7)

a>b(6)>e(12)>g(15) : 확장순서가 더 빠른 방법이 있음

 

 

---

 

 

인공지능의 초기 연구는

'인간이 지능적으로 문제를 해결하는 과정을 어떻게 컴퓨터를 이용할 수 있을까'에 초점을 맞추며

이를 위해 우선 해결해야 할 문제를 컴퓨터를 통해 표현해야 한다.

 

이것은 외부 세계를 컴퓨터에 적절한 형식으로 모델링하는 것이며

- 문제를 풀이하는 과정에서 변화되는 상태를 표현

- 이러한 상태를 변화시키는 적절한 수단을 정의

하는 것을 포함한다.

알고리즘으로 해결하기 어려운 문제를 풀이하는 것은

상태공간에서 목표에 이르는 경로를 탐색하는 것으로 볼 수 있다. 

 

목표상태를 탐색하는 것은 다양한 기준에 따라 순서를 정하여 탐색할 수 있다.